ちょっとTea　Time!?　熱結合なしで熱暴走は押さえられるか？　2021.4.10

パワーアンプを製作するときに必要となるのが終段のパワートランジスタです.
このトランジスターは結構発熱するので、大きな放熱板が必要になりますが、
過加熱が生じないように回路としても熱補償対策が必要です.
　その一つがバイアス電圧発生用のトランジスタの熱結合です.
　最近バイポーラトランジスタで実験しましたが、熱結合がないと初期選定のアイドル電流が数１０分もたてば４倍程度に膨れ上がりました.
それに対して、熱補償（熱結合）があるとアイドル電流はわずかに上昇して一定値になりました.

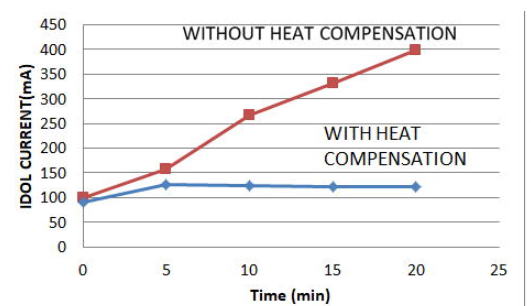
バイポーラを終段にしたときのアイドル電流.熱結合がないとどんどん上昇（いわゆる熱暴走）.


私自身はパワーアンプの終段にはバイポーラではなくてMOSFET派なので、あまり熱暴走は気にしていないところがあって
熱結合を省略したりします.でも、バイポーラを使うときは、ちゃんと熱結合しています（下図）.


高精度アンプをつかった実装ではバイアス電圧発生用トランジスタと共締めで熱結合です.

熱暴走の原因は

　定性的にはトランジスタの見かけ上の抵抗が負特性、すなわち温度があがると抵抗が下がることにあります．
そのため一旦発熱すると電流が増大してさらに温度が上がって電流が増大して、これを繰り返して熱暴走する、
というものです．簡単にはこのように書かれる場合が多いです.
　もうすこし詳しく書くと、温度が上がるとトランジスタのVBE（ベースとエミッタ間電圧）が低下するので
一定の電圧がかかっていると、温度が上がるとより多くの電流が流れてしまう、ということになります.

　でも、バイポーラトランジスタを使えば必ず熱暴走が起こる可能性があるのか？と言われれば、
回路上で対策してある場合が多いです.

　下図はアンプの終段の周辺回路を示したものです．先に温度が上昇するとトランジスタのVBEが低下について
言及しましたが、電流が増える（温度が上昇）ことでVBEを下げる熱暴走を防ぐ工夫がいくつかあります.

１つ目は、エミッタ抵抗(R_e)です.トランジスタに流れる電流が増大するとエミッタ抵抗の電圧が上昇しますので、
その分のVBEが低下することになります.

2つ目は、ベ―ス抵抗(R_b)です．トランジスタに流れる電流（コレクタ電流）はベースに流れる電流のhFE倍（電流増幅率）
で決まりますが、ベース抵抗があるとそこでもベース電流が流れて電圧が発生するのでVBEを低下させます.
でも、アンプ回路の中にはベース抵抗を省略させているものも多く見受けれラれます.ちなみにPA-A２Nでも
ベース抵抗はありません.

３つ目は、放熱板です.仮に放熱板が無限の性能があるとすればトランジスタの温度上昇はありません.


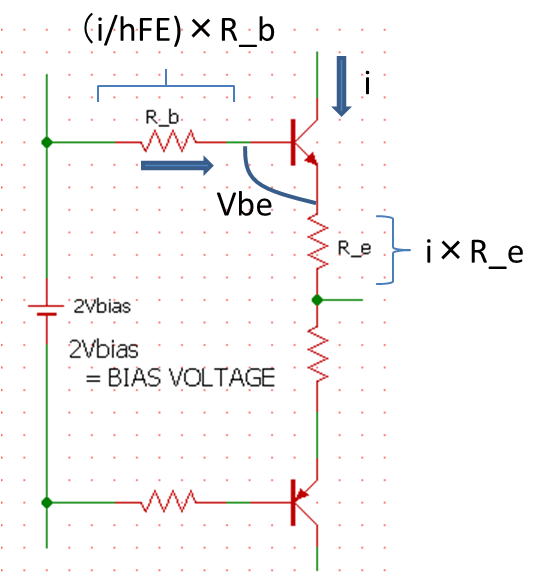
終段のトランジスタに電流が増大したときにVbe電圧を下げる工夫が回路にはあります．

定量的にみてみよう！

では、バイポーラトランジスタを使った場合に、熱結合なしても熱暴走しない条件ってどういったものがあるのか
すこし具体的に検討してみましょう．というのも、熱結合が無ければ実装がすこしでも簡単になりますからね．
ここでは簡単にトランジスターのベース抵抗が無い場合で考えてみましょう.

まずは、終段につかるトランジスタを2SC5200と仮定して、温度に対するVbeの特性をデータシートから読み取りました.

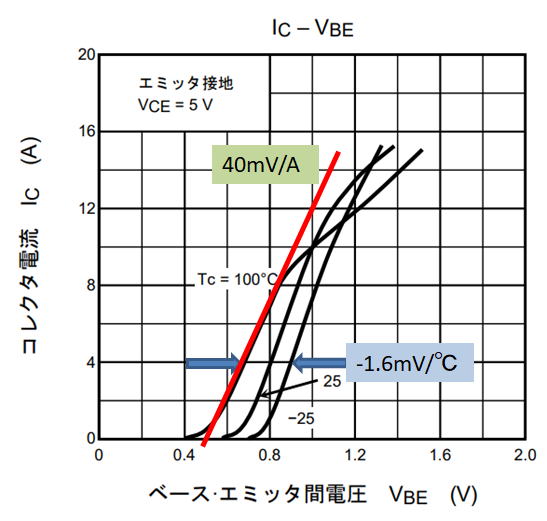
２SC5200のデータシートから抽出

上図からVbeの特性は下式のようになります.Vbeの初期電圧を0.6Vとしています.

　　Vbe＝　0.6＋0.04×ΔI-0.0016×ΔT　（V）
　　ここで
　　　ΔI：　初期アイドル電流から増大したコレクタ電流
　　　ΔT：　初期温度からの上昇温度（℃）

ちなみに、コレクタ電流とＶｂｅの関係は、コレクタ電流による非線形が強いですが、
面倒なので係数の高い40mV/Aとしました.コレクタ電流が小さいところではもっと大きい値になりますが、
まずは安全サイドの係数をつかいます.

放熱板も考える
　熱暴走の有無については放熱板も重要な役割を持ちます.　トランジスタの発熱で上昇する温度ΔTは
簡単にすると次式で近似できます.

　　　ΔT　=　Θ×P
　　　　　　 =　Θ×（Iｃ+ΔＩ） × Vce
　　　　　　 =　Θ×（Iｃ+ΔＩ）　×　{ E - （Iｃ+ΔＩ）　×　Ｒ_e}
　　ここで
　　　　Θ：熱抵抗（℃/W)
　　　　Ｐ：トランジスタの電力損失
　　　　E　：　電源電圧
　　　　Ic　：　トランジスタの初期コレクタ電流
　　　　R_e：　エミッタ抵抗値（Ω）


解くべき式は

最終的に解くべき式は次式のようになるでしょう.Vbiasは初期のバイアス電圧です。

　V_bias　＝　Vbe +　（Ic＋ΔＩ）×R_e　　
　　　　　　＝　0.6 + 0.04×ΔI - 0.0016×ΔT　＋ （Ic＋ΔＩ）×R_e　
　　　　　　＝　0.6 + 0.04×ΔI - 0.0016×【{Θ×（Iｃ+ΔＩ）　×　{ E - （Iｃ+ΔＩ）　×　Ｒ_e}】 　+　（Ic　＋　ΔI）×R_e

ちょうどΔIの２次関数になります.　ΔIに正の解があればΔIで平衡状態になります.　反対にΔIに正の解が無ければ完全な熱暴走です.
ΔIに正の解があるとしても、大きな値で放熱板の温度が異常になるようなら熱暴走と同じですね.

さて、計算は高校生数学ですが、ちょっと面倒なのでまた後日.

計算してみましょう

ΔIは２次方程式になりますが、それを解く公式を忘れてしまっているので、WEBで検索しました（笑。
高校生に笑われそうです。

計算条件

計算のパラメータはいくつもありますが、下記としました。なお電源電圧は24Vとしています。

　エミッタ抵抗：　０．１Ω　〜　１００Ω
　　　　　　　　　　パワーアンプからヘッドホンアンプ、そしてプリアンプを意識して幅広く設定です。

　アイドル初期電流：　1mA　〜　1A
　　　　　　　　　　これはパワーアンプではA級やAB級、そしてプリにつかうような1mA程度の場合も含めて設定です。

　放熱抵抗　：　０．５℃/W〜２００℃/W
　　　　　　　　　　これも大型放熱板からTO-220パッケージそのまままでを想定しています。

計算方法
　計算では平衡状態となるアイドル電流と放熱板温度を計算しています。そして、アイドル電流については
　初期設定値から２倍以内、そして放熱板温度については４０℃以内を安全エリアとしてハッチングしています。
　実用するなら、アイドル電流ならびに放熱板温度の両方があハッチングされているエリアということになります。
　アイドル電流については初期設定から２倍を超えるようなら熱暴走の危険有りと推定です.放熱板温度については
　熱暴走がおこらなくても、あまり温度が上がると素子寿命にも影響するのでほんのり暖かいレベルを限界とします.
　なお、放熱板の熱抵抗はトランジスタ１個あたり値なのでコンプリで使うなら必要とされる熱抵抗はその半分になります。

計算結果

（１）エミッタ抵抗　０．１Ωの場合
　　ちょうどパワーアンプを意識しています。０．１Ωはかなり低い値なので、あまりつかいませんが作例としてはぼちぼちみかけます。
　　この場合では、アイドル電流と放熱板の両方を満たすとすれば１℃／Ｗより小さい大型の放熱板が必要です。
　　大型の放熱板がないと、簡単に熱暴走してしまいます。

　　


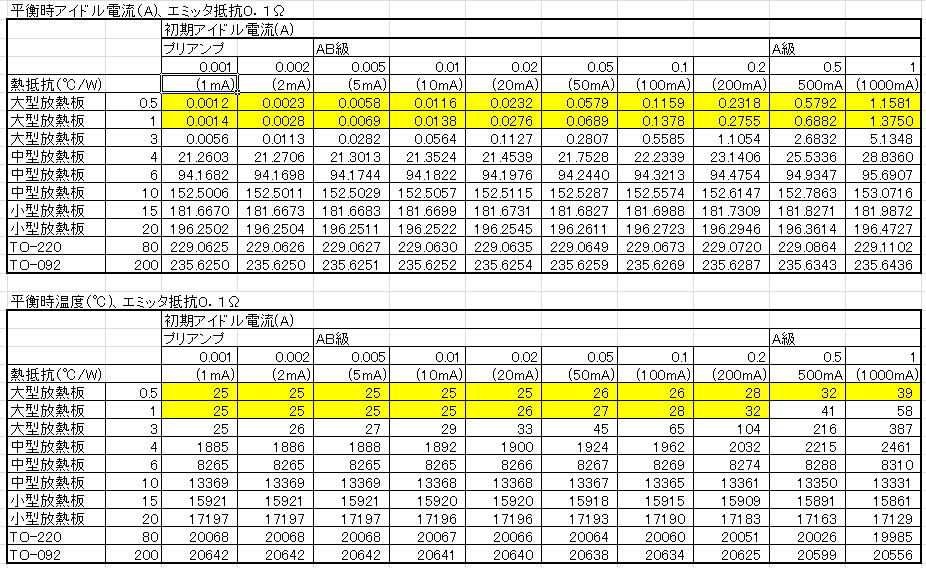
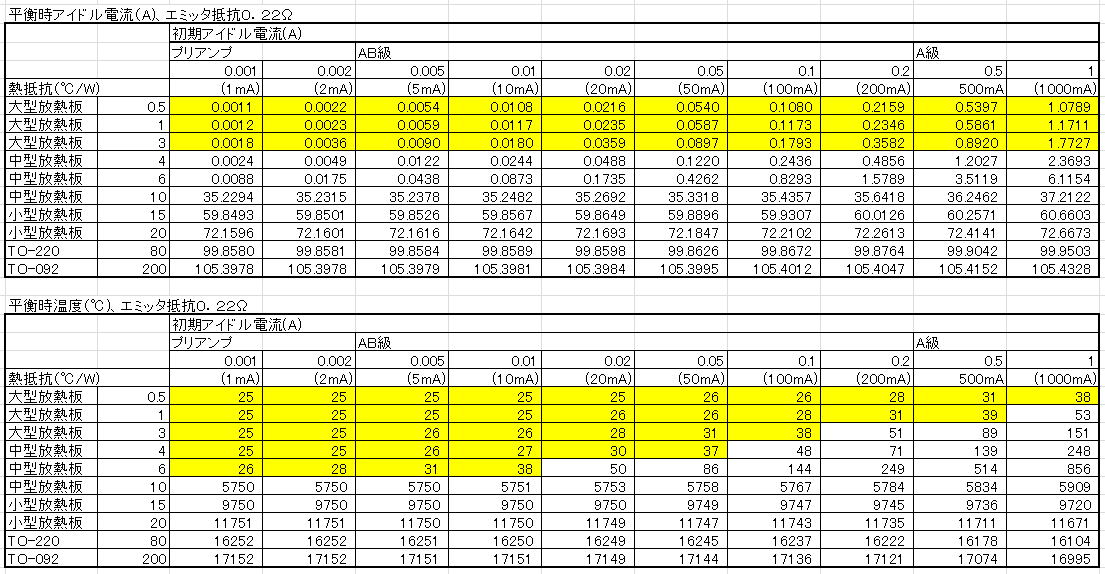
（２）エミッタ抵抗０．２２Ωの場合
　　パワーアンプだとエミッタ―抵抗はこのあたりの値が多いと思います。
　　中型の放熱板でもアイドル電流を10mA程度に押さえれば、なんとか熱結合なしてもいけるでしょう。
　　ただし、中型の放熱板をつけたとしても、気を抜くとすぐに熱暴走します。

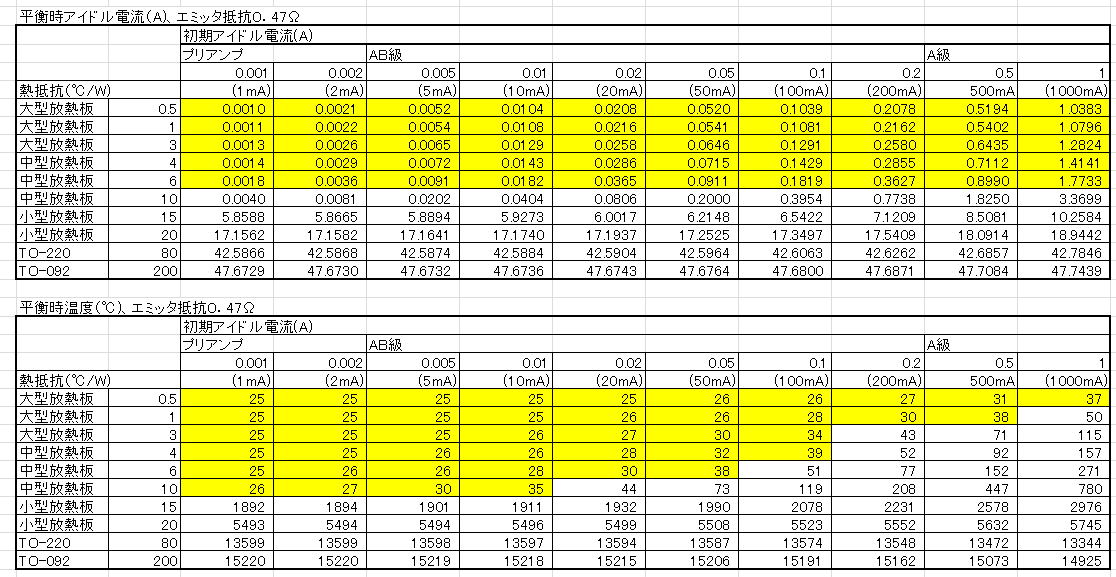
（３）エミッタ抵抗０．４７Ωの場合
　　パワーアンプだとエミッタ―抵抗はこのあたりの値も多いと思います。
　　中型の放熱板でもアイドル電流を10mA程度に押さえれば、なんとか熱結合なしてもいけますがエミッタ抵抗が0.22Ωの場合と安全領域は大きくは変わらないようです。
　　しかし、0.47Ωにするだけで熱暴走しない領域が拡大されます。パワーアンプを製作する場合はこのくらいのエミッタ抵抗値をつかうのが安全でしょう。



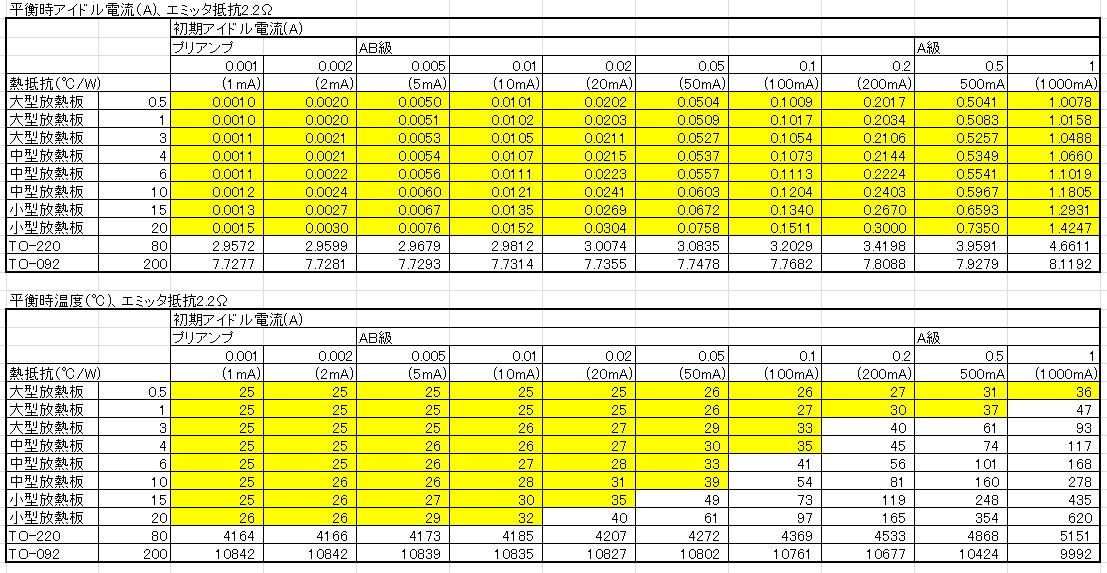
（４）エミッタ抵抗２．２Ωの場合
　ヘッドホンアンプだとこのくらいの値が使われるでしょう。実際にはもうちょっと大きい４．７Ωあたりが多いかもしれません。
　ここまで大きくなると小型の放熱板でも熱結合なくても熱暴走は発生しません。しかし、初期アイドル電流は10mA以下にすることが必要です。
　それ以上だとかなり放熱板が熱くなります。間違っても初期アイドル電流を100mAも流そうものなら焼損しかねません。



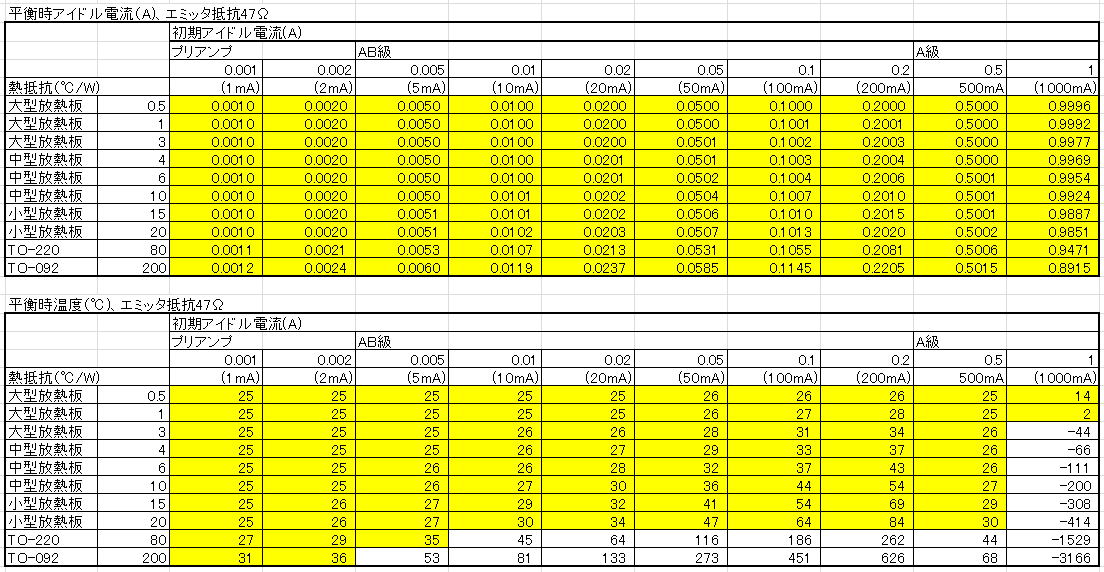
（５）エミッタ抵抗４７Ωの場合
　これはプリアンプをイメージしています。アイドル電流は1mAも流さない程度になるでしょう。
　ここまでエミッタ抵抗を大きくすると、熱暴走でアイドル電流が過剰に大きくなることはありません。
　アイドル電流が1〜２mA程度ならTO-92のトランジスタを裸のままで使用することができます。
　ちょうど、プリアンプのトランジスタにはなにもしないか、あるいは小型の放熱板が取り付けられているだけで、とくに熱結合がされていないことが理解できます。



結論

　今回はバイポーラトランジスタをアンプの終段に用いたときに、熱結合ななくても熱暴走しない条件を試算してみました。

　・パワーアンプではエミッタ抵抗値が0.22Ω以下では放熱板が中型サイズ以上にしないと、アイドル電流を多めに流すと熱暴走の危険があります。反対に熱結合しないのなら、
　　アイドル電流は10mA程度の設定が望ましいといえるでｈそう。
　・ヘッドホンアンプも基本的には熱暴走はなさそうです。ただしアイドル電流の放熱のために小型の放熱板は必要です。初期アイドル電流も10mA程度に押さえたほうがいいでしょう。
　・プリアンプは基本的に熱暴走はしないでしょう。ただし、アイドル電流による放熱対策は必要です。

いままで、熱暴走対策は経験的に定性的におこなっていましたが、今回の検討ですこし定量的に整理できたような気がします。

（おしまい）